等边三角形ABC外接圆上一点P,连接PA、PB和PC,可以得出如下五个结论:
- PA=PB+PC。如下图,
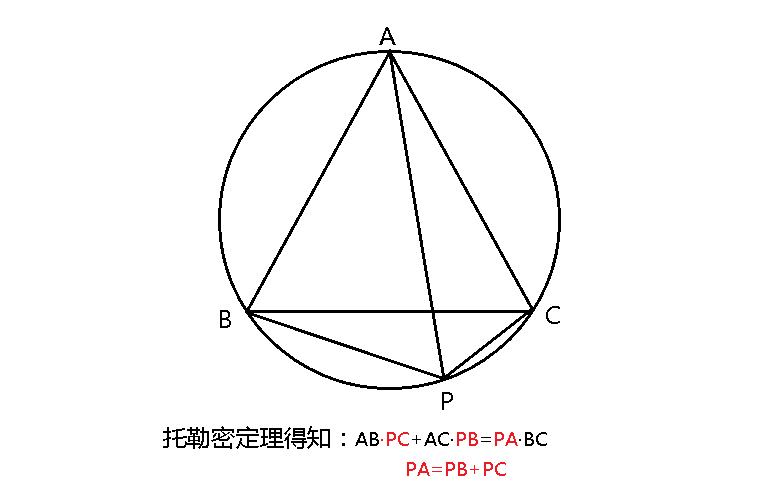
2.PA交BC于M,则1/PM=1/PB+1/PC。
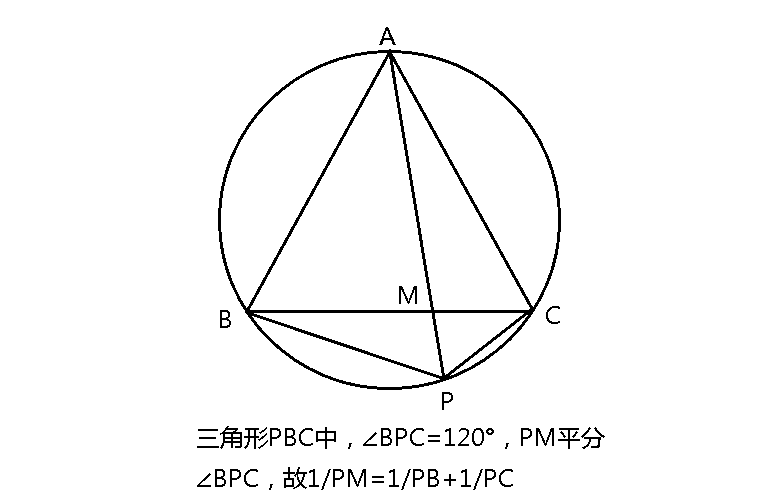
3.PB·PC=PM·PA。系由1/PM=1/PB+1/PC公式推导而来。
4.PB²+PC²+PB·PC=BC²。见下图作CN垂直于BP延长线,PN=1/2 PC,CN=√3/2 PC,BC²=BN²+NC²=(PB+PN) ²+NC²,将PN、CN代入即可。

5.PA²+PB²+PC²=2BC²。根据上述结论可作如下推导:
PA²+PB²+PC²=(PB+PC)²+PB²+PC²=2PB²+2PC²+2 PB·PC=2(PB²+PC²+PB·PC)=2BC²。
