源码:
https://gitee.com/anjiang2020_admin/fft/blob/master/fft.py
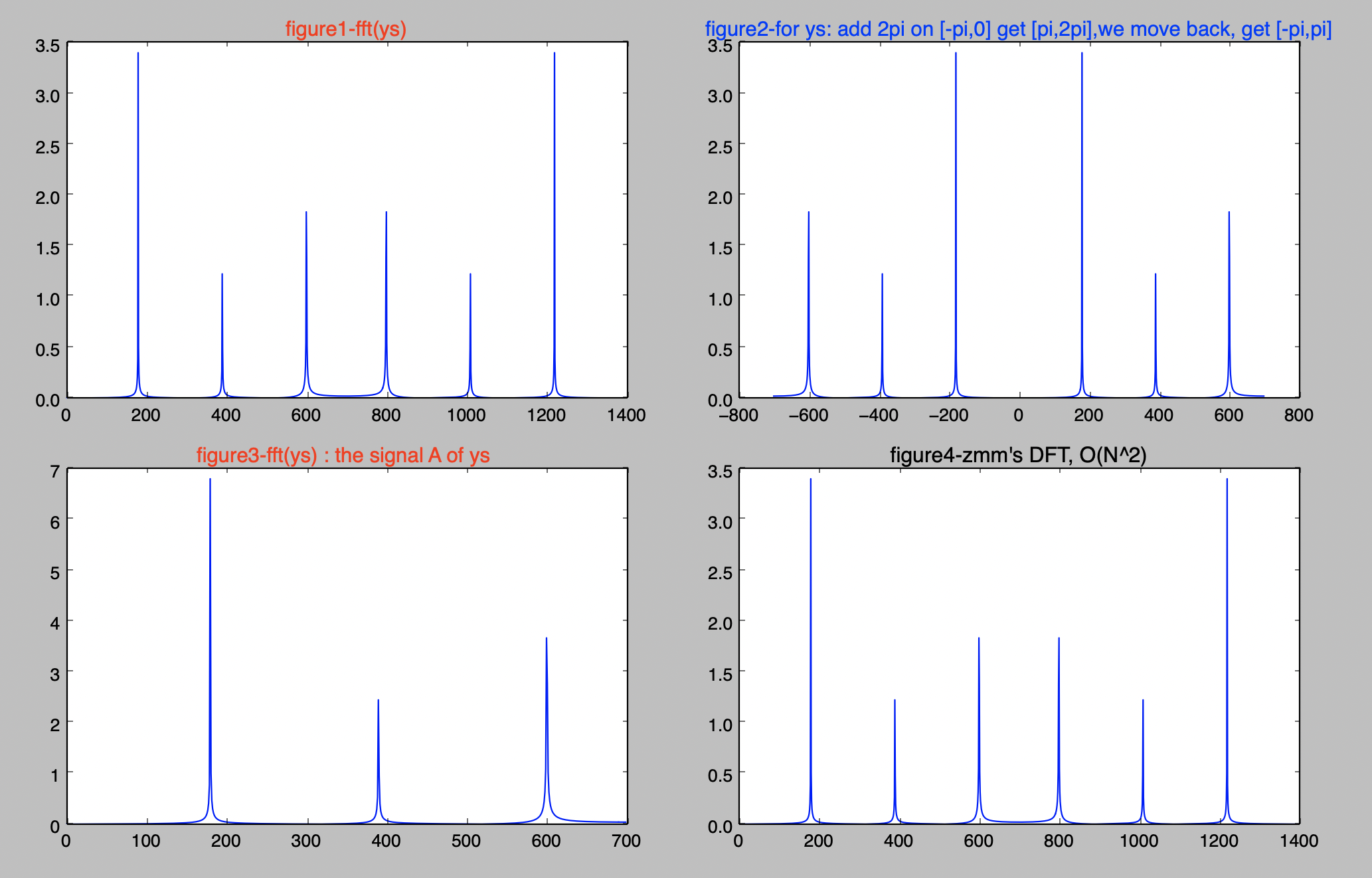
关于图1中4个图的解释:
图1中的figure1
图1中 figure1,为对信号y的采样ys的1400点傅立叶变换
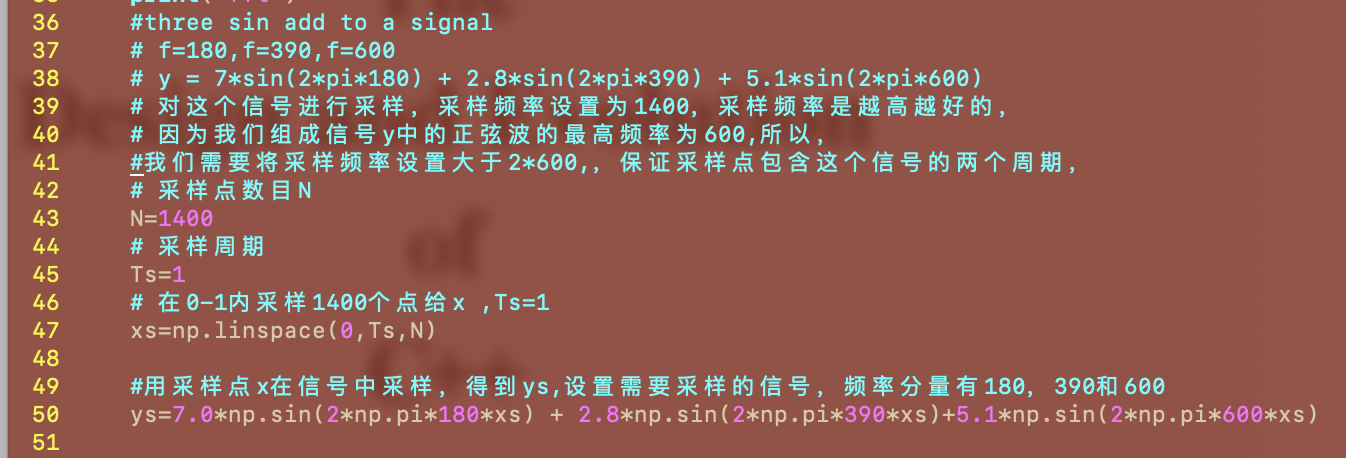
原始信号y是由频率为180,390,600的正弦波叠加而成的。
xs是在[0,1]范围内采样了1400个值。
采样信号ys是对y在[0,1]范围内,采样1400个值得到。
我们观察图1中的figure3,频谱信号在180,390,600处是峰值,频谱信号正确描述了ys的组成分量,并且三个峰值比较接近:7.0,2.8,5.1,这也印证了一个结论:信号是由若干个正弦波叠加而成的,傅立叶变换能够把这些叠加成某信号的正弦波的频率和幅值找出来。
图1中的figure2:
傅立叶变换默认是对信号ys在一个周期T内的信号进行计算得到其内含有某频率正弦信号的幅值的。这个某频率通常表达成:k/(N*Ts),N为采样点数目,Ts为采样间隔,Ts,time of sampling.由于我们在[0,1]范围内采样了1400个值。N=1400,Ts=(1-0)/1400=1/1400,所以,频率表达成k/(N*Ts)=k. 而这个N*Ts就是采样的总时长,这个总时长就是信号ys的一个周期,1/N*Ts就是信号ys的频率.
所以,这个某频率又被表达成k倍的ys的频率1/N*Ts。这个频率转换成角频率就是2*pi*k/N*Ts,由于在傅立叶变换离散化的时候,Ts被消去了,如下:

图3 傅立叶变换的离散化
所以,在计算k时的傅立叶变换时,是使用角频率为2*pi*k/N的n倍的一组信号与n时的f值(ys值),对应相乘得到的 。
设N=1400,
计算F(k)时,是以2*pi*k/N角频率的信号为基础的
计算F(0)时,是以2*piI*0/N=0角频率的信号为基础的
计算F(1)时,是以2*pi*k/N=2*pi*1/1400角频率的信号为基础的
计算F(4)时,是以2*pi*k/N=2*pi*4/1400角频率的信号为基础的
计算F(N)时,是以2*pi*N/N=2*pi角频率的信号为基础的
计算F(N+1)时,是以2*pi*(N+1)/N=2*pi+ 2*pi*1/1400(以角频率的信号为基础的
注意到:0角频率的信号与 2*pi角频率的信号是一样的. 每秒钟让sin信号的弧度变化0,与每秒钟让sin信号的弧度变化2*pi是等效的。
角频率2*pi*1/1400 与2*pi + 2*pi*1/1400的sin信号也是等效的。
所以,我们计算F时,k取值为[0,N-1]即可。
所以,N越大,我们可以求取的k才会越大,k越大意味着组成原始信号ys的sin信号的频率越大,越能分解到ys的细节。
k取值为[0,N-1],意味着对应的角频率为[0,2*pi], 那么这个角频率等效于[-pi,pi],离散傅立叶变换的反变换本是要从负无穷到正无穷的角频率都要积分的,离散化后就是一个周期内:[-pi,pi],故,角频率范围[-pi,pi]才更加符合离散化的傅立叶变换。
但是,我们求得的F(k),一共N个,它是对应于[0,2*pi]的,如何让F(k)对应到[-pi,pi]上呢?
答:把F(k)中对应[pi,2*pi]的项,直接对应给[-pi,0]即可。
F(k)对于应于[0,2*pi],可以将其一分为二:
F(k)前半部分--->[0,pi],F(k)后半部分--->[pi,2*pi]
故:F(k)的后半部分 --->[-pi,0]
故[-pi,pi] 对应于 [F(k)的后半部分,F(k)的前半部分],这就是图1中figure2的内容。
关于图1中的figure3:
此图中的3个峰值刚好对应了组成信号ys的三个sin信号的幅值。
在得到图1中的figure2后,将figure2中的-180对应的值与180对应的值加起来,就得到了图1中figure3中,180对应的峰值。
为什么要这样做?
因为频率为-180在现实中是无意义的,但是在公式中是可以存在的。所以,直接按照公式计算时,就把频率为180的信号的幅值平均分配给了180度的信号和-180频率的信号。所以,我们就把 abs(频率)一样的信号对应的幅值加起来,就得到了真实180频率的信号的幅值。【这个解释很不直观,以后我再想办法解释得更清晰]
关于图1中的figure4:
按照图3中的公式(1),写一个n的for循环,就得到F(k),
当k=0,1,2,....,N-1时,就需要写N个n的for循环了。
figure 4就是我么写了N个n的for循环得到的结果。
这个结果跟图1中的figure1是完全一样的。完全一样的?为什么要写这个呢?
因为图1中的 figure1是用快速傅立叶变换FFT得到的,调用的是scipy中的fft函数
from scipy.fftpack import fft
然后,对ys直接使用fft函数:

而图1中的figure4是用公式1自己实现的:
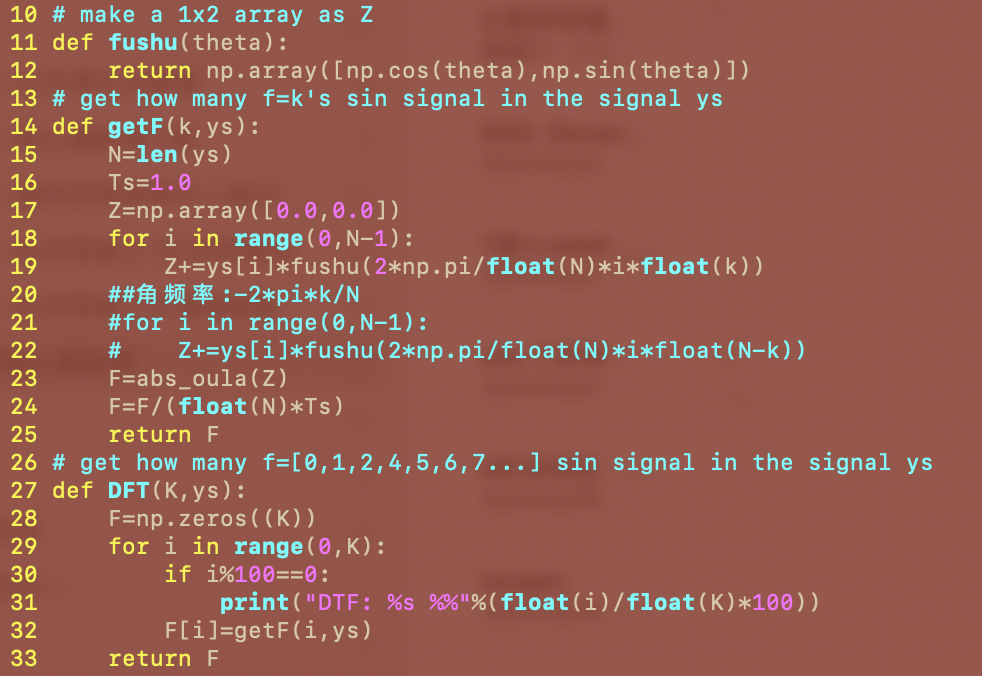
这里getF是得到F(k)的for循环。DFT是得到k=0,1,2,...N-1的for循环。DFT即使离散傅立叶变换。
显然DFT很简单,两个for循环就可以了,那为什么还要有FFT函数呢?
因为两个for循环太慢了,要加速,使其Fast
使用了加速计算的方法,所以叫Fast -DFT,简称:FFT
这个加速运算就是蝶形运算了,蝶形运算主要利用了这样一个性质:


计算F(k)和计算F(k+N/2)是不是有某种联系呢?
是不是计算完其中一个,比如F(k),就可以大大简化F(k+N/2)的计算了呢?

上图中,要计算F(1),F(2),...F(16),只用计算F(1),F(2),...F(8)即可,我们把这个过程叫奇偶分解。

奇偶分解法使用后,降低了一半的乘法计算量。f(n)*w(n,k)算一次乘法。
本来是16*16次乘法,减少到了1*16*8次,含有偶数部分的8x8次乘法和奇数部分的8x8次乘法。
本来16*15次加法, 变为:16+ 2*8*7。
观察下F(1)至F(8)的计算过程,发现它的偶数部分可以做奇偶分解,它的奇数部分也可以做奇偶分解。
偶数部分[8个值] 做奇偶分解:将偶数部分原本需要的8*8次乘法降到了8*4次,其中含分解得到的偶数部分的4*4次和奇数部分的4*4
奇数部分做奇偶分解:将奇数部分原本需要的8*8次乘法降到了8*4次。其中含分解得到的偶数部分的4*4次和奇数部分的4*4
总的乘法计算量由1x16*8变为2x8x4.
总的加法计算量由16+2*8*7 变为16+2x(8+2*4*3)
继续对偶数部分的偶数部分[4个值]做奇偶分解,乘法次数由4*4,降低为4*2,其中含分解得到的偶数部分的2*2次和奇数部分的2*2
继续对偶数部分的奇数部分做奇偶分解,乘法次数由4*4,降低为4*2,其中含分解得到的偶数部分的2*2次和奇数部分的2*2
继续对奇数部分的偶数部分做奇偶分解,乘法次数由4*4,降低为4*2,其中含分解得到的偶数部分的2*2次和奇数部分的2*2
继续对奇数部分的奇数部分做奇偶分解,乘法次数由4*4,降低为4*2其中含分解得到的偶数部分的2*2次和奇数部分的2*2
总的乘法计算量由2x8x4变为4x4x2.
总的加法计算量由16+2*8*7 变为16+2x(8+2*4*3)变为16+2x(8+2*[ 4+2*2*1 ])
继续对偶数部分的偶数部分 的偶数部分 做奇偶分解,乘法次数由2*2降低为2*1,其中分解得到的偶数部分1*1次和奇数部分的1*1次。
继续对偶数部分的偶数部分 的奇数部分 做奇偶分解,乘法次数由2*2降低为2*1,其中分解得到的偶数部分1*1次和奇数部分的1*1次。
继续对偶数部分的奇数部分 的偶数部分 做奇偶分解,乘法次数由2*2降低为2*1,其中分解得到的偶数部分1*1次和奇数部分的1*1次。
继续对偶数部分的奇数部分 的奇数部分 做奇偶分解,乘法次数由2*2降低为2*1,其中分解得到的偶数部分1*1次和奇数部分的1*1次。
继续对奇数部分的偶数部分 的偶数部分 做奇偶分解,乘法次数由2*2降低为2*1,其中分解得到的偶数部分1*1次和奇数部分的1*1次。
继续对奇数部分的偶数部分 的奇数部分 做奇偶分解,乘法次数由2*2降低为2*1,其中分解得到的偶数部分1*1次和奇数部分的1*1次。
继续对奇数部分的奇数部分 的偶数部分 做奇偶分解,乘法次数由2*2降低为2*1,其中分解得到的偶数部分1*1次和奇数部分的1*1次。
继续对奇数部分的奇数部分 的奇数部分 做奇偶分解,乘法次数由2*2降低为2*1,其中分解得到的偶数部分1*1次和奇数部分的1*1次。总的乘法计算量由4x4x2变为8x2x1.
总的乘法计算量由4x4x2变为8x2x1.
无法再奇偶分解了。
总的来说,原来乘法次数为:16x16, 现乘法次数为:16次=N
总的加法计算量16+2x(8+2*[ 4+2*2*1 ])不变。
加法计算的量计算的过程是个递归的过程:
本来16*15次加法, 变为:16+ 2*8*7。注意到这里有个f(N)=N*(N-1)存在。我们用f(N)于f(N/2)来表达:
N*(N-1) ----> N + 2*(N/2)*(N/2-1),
f(N)=N+2*f(N/2)
N=16开始递归,到N/2-1=0结束,当N=16,8,4时可递归,一共递归3次
f(N)=N+2*f(N/2)
=N+2*(N/2+2*f(N/4))
=N +2*(N/2+2*[ N/4+2*f(N/8) ])
=N +2*(N/2+2*[ N/4+2*f(N/8) ])
=3N+8*f(N/8)=3N+8*N/8=4N=log_2_N*N
总结:
原Nx(N-1)次加法,降低为log_2_N*N次加法,
原NxN次乘法,降低为N次。
所以说:蝶形算法极大了提升了计算速度。蝶形算法的源码后续给出。
蝶形计算主要由于F(k)与F(k+N/2)的特殊关系启发,F(k)与F(k+N/2)的特殊关系则由:

引起。
