一、直线
1、直线的倾斜角
在平面直角坐标系中,当直线与x轴重合或平行时,规定倾斜角为0,对于与x轴相交的直线,把x轴绕着交点按逆时针方向转到和直线重合时所转的最小正角叫做直线的倾斜角,倾斜角的范围[0,π)。
2、直线的斜率
- 倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率k,即k=tanα (α≠90°);倾斜角为90°的直线没有斜率。
- 斜率公式:k=Δy/Δx=(y1-y2)/(x1-x2)。
- 直线的方向向量:(1,k)
3、直线的方程
点斜式:
已知直线过点(x0,y0),斜率为k,则直线方程为:y−y0=k(x-x0)。
斜截式:
已知直线在y轴上的截距为b和斜率k,则直线方程为:y=kx+b。
两点式:
已知直线经过(x1,y1),(x2,y2)两点,则直线方程为:
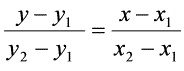
截距式:
已知直线在x轴和y轴上的截距为a,b,则直线方程为:x/a+y/b=1
一般式:
任何直线均可写成:Ax+By+C=0(A,B不同时为0)的形式。
4、点到直线的距离及两平行直线的距离
点P(x0,y0)到直线Ax+By+C=0的距离:
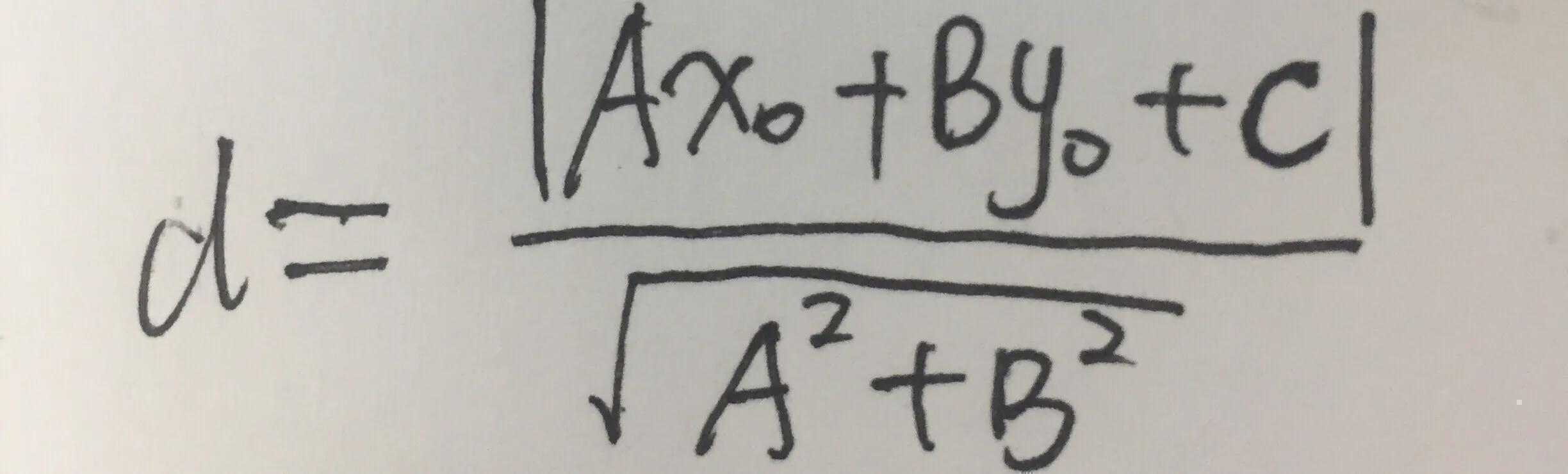
两平行线Ax+By+C1=0和Ax+By+C2=0间的距离为:
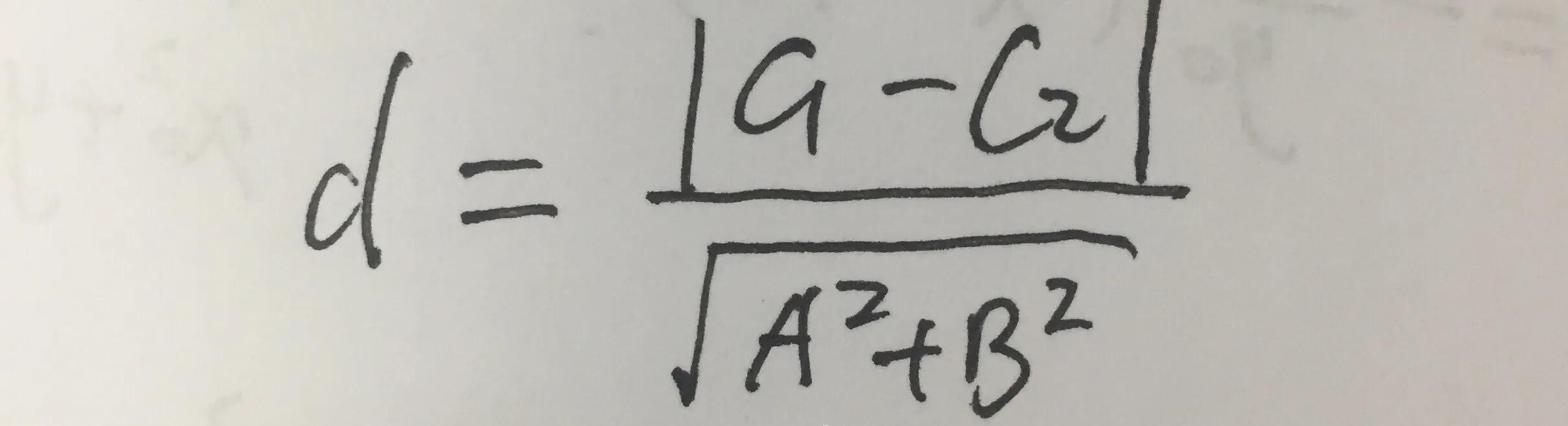
5、直线与直线的位置关系
直线ax+by+c=0与直线Ax+By+C=0的位置关系:
- 平行:aB−Ab=0且bC−Bc≠0。
- 相交:aB−Ab≠0。
- 重合:aB−Ab=0且bC−Bc=0。
- 垂直:aA+bB=0。
6、夹角公式
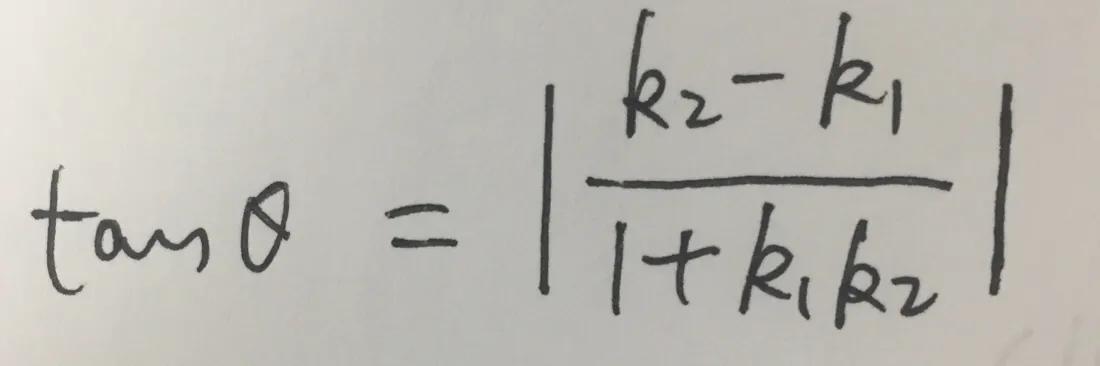
(k1k2≠−1)。
例:已知点M是直线2x−y−4=0与x轴的交点,把直线绕点M逆时针方向旋转45°,得到的直线方程是3x+y−6=0。
7、对称问题
点关于点对称:利用中点坐标求解。
如求点A(2,2)关于点B(3,1)对称的点C,由A与C的横坐标之和等于B点横坐标的二倍,A与C的纵坐标之和等于B点纵坐标的二倍,得C(4,0)。
点关于直线对称:利用垂直平分线求解。
如求点M(2,2)关于直线l:y=2x+1对称的点N,即直线l为线段MN的垂直平分线。由M、N的中点在直线l上,且直线MN与l垂直,斜率之积为-1(斜率不存在时,利用平移求解),联立求解出点N坐标。
直线关于点对称:设直线系方程,再通过点到两直线的距离相等,或直线上点关于点对称来求解。
如求2x+3y+4=0关于点(3,3)对称的直线l,可设l为:2x+3y+c=0,由点(3,3)到两条直线的距离相等,代入距离公式得c=-34并得到直线方程2x+3y-34=0;也可任取直线上一点,如(1,-2),得到该点关于(3,3)对称点(5,8)并代入l方程解得c=-34及直线方程2x+3y-34=0。
直线关于直线对称:采用到角公式求解(关于平行直线对称可利用平移求解)。
(k1-k2)/(1+k1·k2)=(k2-k3)/(1+k2·k3)
已知k1、k2求解出k3,再结合交点求出直线方程。
另可采用直线的方向向量结合旋转求解出斜率。

二、圆
1、圆的方程
标准方程:
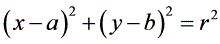
一般方程:
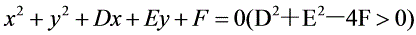
参数方程:

其中θ为参数,圆心为(a,b),半径为r。
2、点与圆的位置关系
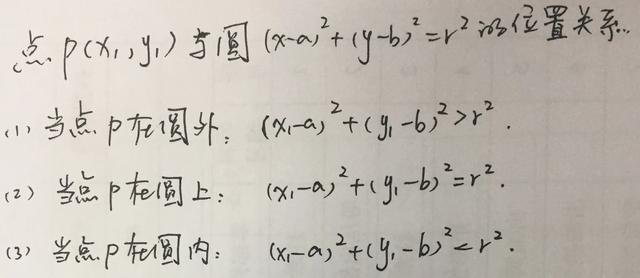
3、直线与圆的位置关系
⑴将直线方程与圆的方程联立,根据方程解的个数,判断直线与圆的位置关系。
相交:若△>0 ,方程有两个根,即直线与圆有两个交点。
相切:若△=0 ,方程有一个根,即直线与圆有一个交点。
相离:若△<0 ,方程有零个根,即直线与圆有零个交点。
⑵将圆心到直线的距离d与圆的半径r比较:
相交:d<r。
相切:d=r。
相离:d>r。
4、圆与圆的位置关系
两圆的位置关系,可通过比较半径与圆心距的大小来判断。
外离:两圆半径和小于圆心距。
外切:两圆半径和等于圆心距。
相交:两圆半径和大于圆心距,半径差小于圆心距。
内切:两圆半径差等于圆心距。
内含:两圆半径差大于圆心距。

5、圆的切线与弦长
⑴圆上点的切线方程

当圆心为(a,b)时,所有的坐标进行平移转换,长度不变。可得到:
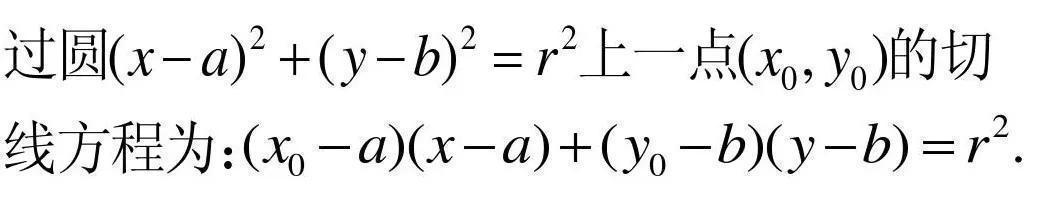
当圆为一般方程时,可得到:
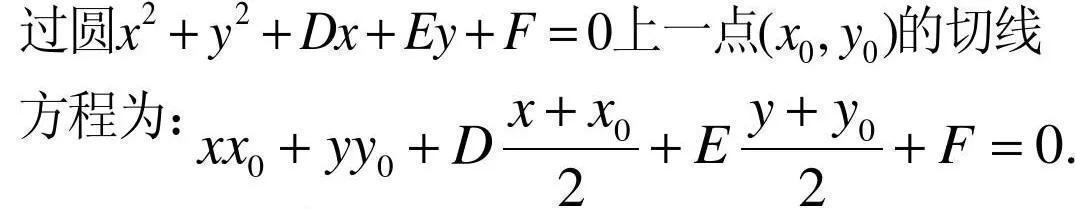
⑵圆外点的切线方程
过圆外一点作圆的切线有两条,设出斜率存在时的方程,利用圆心到直线的距离等于圆的半径求解出切线方程。只有一个解时需考虑斜率不存在的切线。
(3)圆外点的切线长
点与圆心的连线(斜边)、切线(直角边)和半径(直角边)构成的直角三角形采用勾股定理求解切线长。
(4)圆的弦长
几何法:圆心到弦的垂线(直角边d)、弦(l)的一半(直角边)和半径(斜边r)构成的直角三角形采用勾股定理求解弦长。
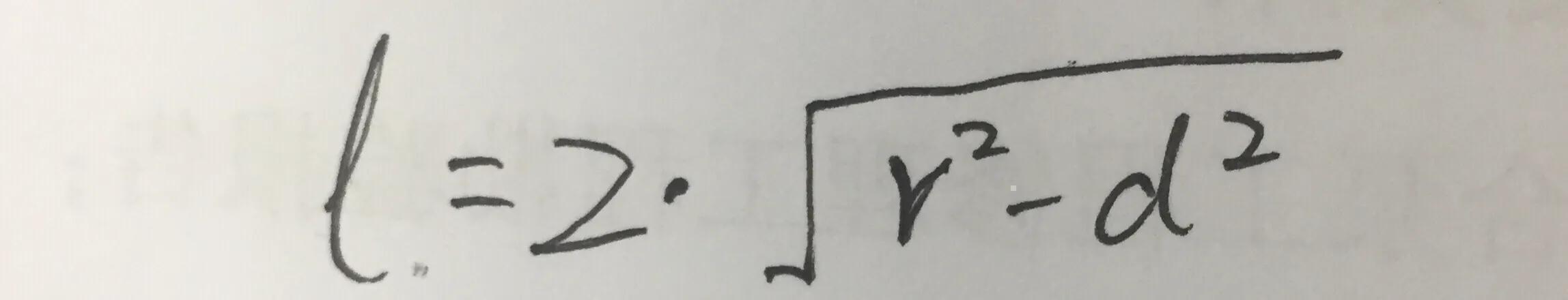
解析法:通过联立圆与直线的方程,根据韦达定理得出两根的关系,可由两点间的距离得到弦长。

